7.4 Алгоритм Шелла
Разработан Дональдом Л. Шеллом в 1959 году.
Этот алгоритм классифицируется как сортировка вставками с убывающим шагом.
В первом проходе попарно переставляются элементы, находящиеся друг от друга на
некотором растоянии, например, 9 позиций. Во втором проходе переставляются элементы,
отстоящие на меньшее число позиций, например, 5. И т. д. На последнем шаге сортируются
соседние элементы. На ранних этапах изучения алгоритма его исследователи отмечали:
"Непонятно как алгоритм работает".
На самом деле принцип убывающих шагов может быть применён для различных базовых сортировок,
в том числе для пузырьковой сортировки. В результате модификации получается
сортировка расчёской.
Эффективность алгоритма заключается в том, что на каждом из промежуточных шагов сортируется либо небольшое число элементов, либо уже достаточно хорошо упорядоченные наборы элементов. Упорядоченность массива возрастает после каждого прохода.
Поведение алгоритма Шелла до конца не исследовано до сих пор, в частности, не найдено универсальное решение проблемы выбора последовательности изменения шага. Исследование алгоритма привело к формулированию нескольких теорем.
Эффективность алгоритма проявляется даже в случае всего двух проходов с шагами h и 1. Время работы в этом случае зависит от размера массива как
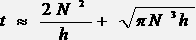 .
.А лучшее значение шага h оказывается равным
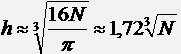 ,
,следствием этого является зависимость времени работы от размера массива, которую можно выразить как
При большем числе проходов эффективность повышается. Тем не менее, в процессе изучения алгоритма был обнаружен порог эффективности, который долго не удавалось преодолеть (барьер N1,5). Этот барьер можно преодолеть подбором шагов.
Изменение массива при сортировке по алгоритму Шелла будет имеет вид:

В ходе изучения алгоритма исследовалась зависимость среднего числа перестановок от размера массивов при 100 <= N <= 60000 для нескольких типов последовательностей шагов, для которых были получены соответствующие зависимости времени работ от размера массива:
2k+1, ..., 9, 5, 3, 1 => 1,09N1,27
2k−1, ..., 15, 7, 3, 1 => 1,22N1,26
(2k−(−1)k)/3, ..., 11, 5, 3, 1 => 1,12N1,28
(3k−1)/2, ..., 40, 13, 4, 1 => 1,66N1,25
Общую формулу можно выразить как
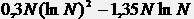
или, упростив, как
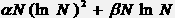
или 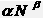 .
.
Распространённой (хотя и далеко не самой эффективной) является последовательность шагов 9, 5, 3, 2, 1.
Кроме указанных формул используются числа Фибоначчи.
Рекомендуется избегать последовательности шагов в виде степеней двойки (..., 16, 8, 4, 2, 1), так как это снижает эффективность алгоритма (хотя сортировка выполняется и в этом случае). Последний шаг обязательно должен быть единичным.
Один из рекомендуемых вариантов выбора последовательности шагов: принять шаги последнего и
каждого предыдущего этапов h1 = 1,
hs + 1 = 3hs + 1,
и остановиться на некотором шаге ht
, когда ht + 2 ≥ N.
В итоге получается
последовательность шагов ..., 121, 40, 13, 4, 1 (такая же, как в случае (3k−1)/2),
которая является одной из самых эффективных. Возможны и другие, эвристически подбираемые последовательности
шагов, ещё более эффективные (например, 120, 40, 12, 4, 1).
Возможен также расчёт шага первого этапа, исходя из размера массива, и уменьшение
шага вдвое на каждом следующем этапе.
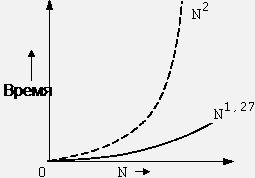
Сравнение зависимости времени работы для алгоритма Шелла и N-квадратичных алгоритмов.
Процедура сортировки методом Шелла на языке "Паскаль"var
x:char; a:array[0..4] of integer;
a[1]:=5; a[2]:=3; a[3]:=2; a[4]:=1; for k:=0 to 4 do begin
for i:=h to n-1 do begin
j:=i-h; while (x<item[j]) and (j>=1) do begin
j:=j-h item[j+h]:=x Аналогичная процедура на Си/Си++void Shell_sort(char* item,int n) { int step[ST]={120,40,12,4,1}; // Массив убывающих шагов int i,j,k,h; char buf; for(k=0; k<ST ;k++) { h=step[k]; for(i=h; i<n; i++) { buf=item[i]; for(j=i-h; buf<item[j] && j>=0; j-=h) item[j+h]=item[j]; item[j+h]=buf; } } } |
Проверка условия j>=1 (для Паскаля или j>=0 для Си/Си++) предотвращает выход за пределы массива. Считается, что такие дополнительные проверки слегка снижают производительность алгоритма.