7.2 Сортировка отбором
Другое название − сортировка выбором.
В структуре данных (массиве или списке) ищется наименьший (или наибольший) элемент
и меняется местами с первым (или с последним, в зависимости от направления упорядоченности).
(Здесь сочетаются 2 процесса − поиск и обмен.) Затем из оставшихся N
− 1 элементов ищется наименьший и меняется местами со вторым. Процесс
повторяется до тех пор, пока нечего будет переставлять (т.е. пока структура данных
не исчерпается).
При реализации алгоритма желательно оптимальным образом совместить процессы поиска минимума и обмена, для достижения максимальной эффективности.
Процедура сортировки простым или прямым выбором на языке "Паскаль"var
t:char;
begin
c:=a; t:=item[a]; for b:=a+1 to n do
begin
t:=item[b]; ssign:=1 begin
item[a]:=t Такая же процедура на языках C/C++{ int a,b,c; char buf; int change; for(a=0; a<n-1; ++a) { buf=item[a]; // Текущий минимум c=a; // Индекс минимума change=0; // Признак обмена for(b=a+1; b<n; ++b) if(item[b] < buf) { buf=item[b]; // Начало обмена c=b; // Новый минимум change=1; // Признак обмена } if(change) { item[c]=item[a]; // Продолжение обмена item[a]=buf; } } } |
Фактически в этих процедурах во внешнем цикле устанавливается нижняя граница
интервала анализа и элемент с таким индексом принимается за опорный. Во внутреннем
цикле каждый из оставшихся элементов сравнивается с опорным и если условие сравнения
выполняется, найденный локальный минимум фиксируется в буфере (принимается за новый
опорный) и устанавливается в "1" признак обмена.
В продолжении внешнего цикла происходит обмен, если признак равен "1". Эффективность
алгоритма повышается за счёт разнесения операции обмена по разным циклам (по сравнению
с пузырьковой сортировкой).
Иллюстрация работы алгоритма.
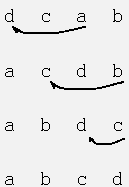
Здесь хорошо виден такой же "треугольный" характер, что и у пузырьковой сортировки.
Этот алгоритм так же является N-квадратичным. Внешний цикл выполняется N − 1 раз,
внутренний − N/2 раз, каждая полная перестановка требует трех операций присваивания.
Число операций сравнения и перестановки (присваивания):
(N2 − N)/2 сравнений
N − 1 присваиваний в лучшем случае
N(log2N + y) присваиваний в среднем случае
N2/4 + 3(N − 1) присваиваний в худшем случае
y~0,577216 − константа Эйлера
Другой, более простой, но менее эффективный вариант реализации выполняет
3(N − 1) присваиваний в лучшем случае.
При одинаковом числе сравнений, сортировка отбором эффективнее пузырьковой в среднем случае за счёт наличия логарифма в выражении для числа перестановок.
К модификациям этого алгоритма относится пирамидальная сортировка. Существует также двунаправленный вариант сортировки отбором, в котором на каждом проходе отыскиваются и устанавливаются на свои места и минимальное, и максимальное значения.