6. Двоичные деревья

Типы деревьев: Двоичные (бинарные), ориентированные, упорядоченные, мультивариантные (дерево Байера).

Дерево - динамическая нелинейная структура данных, каждый элемент которой содержит собственно информацию (или ссылку на то место в памяти ЭВМ, гди хранится информация) и ссылки на несколько (не менее двух) других таких же элементов. Для бинарного дерева таких ссылок две: на правый соседний и левый соседний элементы.

Основные операции, выполняемые над деревьями (те же, что и над списками) - вставка, удаление и поиск элементов.

Преимущество бинарных деревьев: в случае, если дерево отсортировано, то операция поиска выполняется быстро, с эффективностью, близкой к эффективности двоичного поиска.

Чем же отличается бинарное дерево от двусвязного списка?
Иногда ничем, не только от двусвязного, но и от односвязного списка.
Основное отличие - у списка соседними являются предшествующий и последующий элементы, и структура линейна; а у бинарного дерева соседними являются элементы с меньшим и большим ключом, и структура, в общем случае ветвящаяся - в виде дерева, откуда она и получила свое название.

Нужно помнить, что дерево - это только метод логической организации информации в памяти, а память - линейна. В случае, если информация хранится в произвольном (и неизвестном программисту) месте памяти, а ключ и информация - разные понятия (иногда они могут и совпадать), структура элемента дерева может быть представлена следующим образом:

Этой структуре соответствует набор типов языка Паскаль:

type
info=(* тип хранимых данных *);
ptr=^node;
node=record
key:Integer;
left,right:ptr;
data:^info
end;
var
tree:ptr;

Бинарное дерево, образованное такими элементами показано там же.

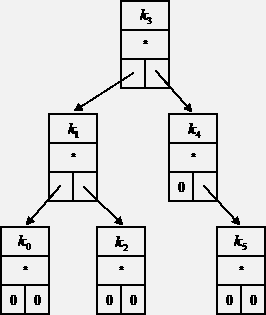
Элемент дерева получил название "узел" (node), иногда его называют листом. Единственный начальный элемент (откуда дерево развивается) - корень (root). Фрагмент (часть) дерева - поддерево или ветвь. Узел, от которого не отходят ветви - конечный или терминальный узел. Количество уровней - высота дерева.

Применение деревьев: для хранения информации, как таковой; в процедурах поиска; для организации файлов на дисковых носителях; в построении эффективных кодов для сжатия информации (коды Шеннона-Фано и Хаффмэна).

Рассмотрим принцип построения дерева при занесении в него информации. Пусть последовательно вводятся записи с ключами 70, 60, 85, 87, 90, 45, 30, 88, 35, 20, 86, 82.

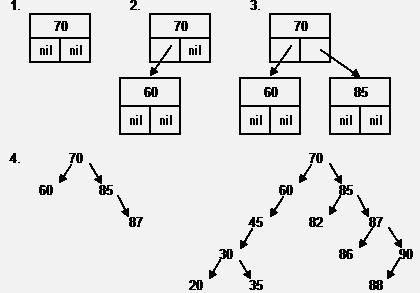
При поступлении очередной записи с ключом k, k сравнивают, начиная с корня, с ключом очередного узла. В зависимости от результата сравнения, процесс продолжают в левой или правой ветви до тех пор, пока не будет достигнут один из узлов, с которым можно связать входящую запись. В зависимости от результата сравнения входящего ключа с ключом этого узла, входящая запись будет размещена слева или справа от него и станет новым терминальным узлом.

Порядок следования узлов дерева зависит от того, каким образом нужно организовать доступ к узлам. Процесс получения доступа ко всем узлам - прохождение дерева.

Существует три способа прохождения дерева:

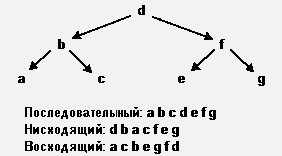
Под корнем здесь понимается как корень всего дерева, так и корень текущей ветви (поддерева).

Хотя бинарное дерево не обязательно должно быть отсортировано, в большинстве практических случаев это требуется.

Порядок сортировки дерева определяется методом, которым дерево будет проходиться.

Максимальный эффект использования дерева достигается, если оно сбалансировано - когда все узлы, кроме терминальных, имеют и правого, и левого соседа; все поддеревья, начинающиеся с одного и того же уровня, имеют одинаковую высоту.

Сбалансированное бинарное дерево - максимально широкое и низкое.

Обратный случай - вырожденное дерево - выродившееся в линейный односвязный список. Такое дерево получается, если заносимые в него данные упорядочены по-возрастанию, или по-убыванию.

Если данные случайны, то получается дерево, приближенное к сбалансированному.

Дерево - рекурсивная структура данных, так как любое поддерево - это тоже дерево. В связи с этим, наиболее эффективными при работе с деревьями оказываются рекурсивные процедуры. Хотя возможно применение и процедур без рекурсии. Рассмотрим разные варианты построения этих процедур.

Рекурсивная процедура добавления узла в дерево на языке "Паскаль" procedure addnode_r(r,prev:ptr; newkey:integer); begin if r=nil then begin new(r); r^.left:=nil; r^.right:=nil; r^.key:=newkey; if tree=nil then tree:=r; {Первый узел} else begin if newkey<prev^.key then prev^.left:=r else prev^.right:=r end; exit end; if newkey<r^.key then addnode_r(r^.left,r,newkey) else addnode_r(r^.right,r,newkey) end;

Процедура вставляет информацию в бинарное дерево, отслеживая ссылки на узлы и выбирая левые или правые ветви, в зависимости от ключа, пока не будет найдено соответствующее место в иерархии дерева.

Аргументы процедуры:

указатель на корень дерева или ветви, в которм ищется место для нового узла;
указатель на предыдущий узел;
ключ;
Сохраняемые данные или указатель на них.

Фактически этот процесс сортирует ключ, прежде чем добавить узел в дерево. Это вариант алгоритма сортировки матодом простых вставок. При построении нового дерева или обслуживании уже упорядоченного дерева рекомендуется добавлять новые узлы именно такой процедурой.

Рекурсивная функция построения идеально сбалансированного дерева с заданным числом узлов на языке "Паскаль" function maketree(n_node:integer):ptr; var newnode:ptr; newkey,nl,nr:integer; begin if n_node=0 then newnode:=nil else begin nl:=n_node div 2; nr:=n_node-nl-1; {Ввод ключа и данных} read(newkey); new(newnode); with newnode^ do begin key:=newkey; left:=maketree(nl); right:=maketree(nr) end; end; maketree:=newnode end; read(n); tree:=maketree(n); {Первый вызов}

Рекурсивные процедуры прохождения дерева в последовательном (inorder), нисходящем (preorder) и восходящем (postorder) порядках на языке "Паскаль" procedure inorder(r:ptr); begin if r=nil then exit; inorder(r^.left); writeln( ... ); {Вывод информации} inorder(r^.right) end; procedure preorder(r:ptr); begin if r=nil then exit; writeln( ... ); {Вывод информации} preorder(r^.left); preorder(r^.right) end; procedure postorder(r:ptr); begin if r=nil then exit; postorder(r^.left); postorder(r^.right) writeln( ... ); {Вывод информации} end;

Аргумент этих процедур - указатель на корень ветви, которую требуется найти. Если нужно найти все дерево, необходим указатель на корень дерева. Выход из рекурсивной процедуры происходит, когда встречается терминальный узел.

Возможно добавление нового узла в дерево и без использования рекурсии:

Нерекурсивная процедура добавления нового узла в дерево на языке "Паскаль" procedure addnode2(skey:integer; var tree:ptr; newdata:^info); var r,s:ptr; t:^info; begin if not searchtree(skey,tree,r) then begin new(t); {Занесение} t:=newdata; {данных} new(s); {новый} s^.key:=skey; s^.left:=nil; {узел} s^.right:=nil; s^.data:=t; if tree=nil then tree:=s else if skey<r^.key then r^.left:=s else r^.right:=s end end;

Поиск в бинарных деревьях выполняется достаточно просто:

Программа поиска в бинарномдереве на языке "Паскаль" function search_tree(skey:integer; var tree,fnode:ptr):boolean; var p,q:ptr; b:boolean; begin b:=false; p:=tree; if tree<>nil then repeat q:=p; if p^.key=skey then b:=true else begin if skey<p^.key then p:=p^.left else p:=p^.right end until (b) or (p=nil); search_tree:=b; fnode:=q; end;

Длительность поиска зависит от структуры дерева. Для сбалансированного дерева (изображено на рисунке) поиск аналогичен двоичному - то есть нужно посмотреть не более Log2N узлов.

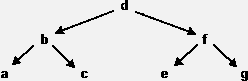
Для вырожденного дерева (изображено на рисунке) поиск аналогичен поиску в односвязном списке - всреднем нужно посмотрет половину узлов.

Удаление узла из дерева - существенно более сложный процесс, чем поиск, так как удаляемый узел может быть корневым, левым или правым. Узел может давать начало другим деревьям (их может быть от 0 до двух).

Наиболее простым случаем является удаление терминального узла, или узла, из которого выходит только одна ветвь.

Для этого достаточно скорректировать соответствующий указатель у предшествующего узла.

Наиболее трудный случай - удаление корневого узла поддерева с двумя ветвями, поскольку приходится корректировать несколько указателей. Нужно найти подходящий узел, который можно было бы вставить на место удаляемого, причем этот подходящий узел должен просто перемещаться. Такой узел всегда существует.

Если это самый правый узел левого поддерева, то для достижения этого узла нужно перейти в следующий от удаляемого узел по левой ветви, а затем переходить в очередные узлы только по левой ветви до тех пор, пока очередной левый указатель не будет равен nil.

Такой узел может иметь не более одной ветви.

Пример удаления из дерева узла с ключом 50.

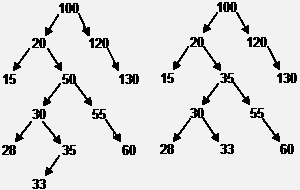
Процедура удаления узла должна различать три случая:

узла с данным ключом в дереве нет;
узел с заданным ключом имеет не более одной ветви;
узел с заданным ключом имеет две ветви.

Процедура удаления узла (автор - Н. Вирт)

Процедура удаления узла двоичного дерева на языке "Паскаль" procedure delnode(var d:ptr; key:integer); var q:ptr; procedure del1(var r:ptr); begin if r^.right=nil then begin q^.key:=r^.key; q^.data:=r^.data; q:=r; r:=r^.left end else del1(r^.right) end; begin if d=nil then exit {Первый случай} else if key<d^.key then delnode(d^.left,key) else if key>d^.key then delnode(d^.right,key) else begin q:=d; {Второй случай} if q^.right=nil then d:=q^.left else if q^.left=nil then d:=q^.right else {Третий случай} del1(q^.left) end end;

Вспомогательная рекурсивная процедура del1 вызывается только в третьем случае. Она проходит дерево до самого правого узла левого поддерева, начиная с удаляемого узла q^, и заменяет значения полей key и data в q^ соответствующими записями полей узла r^. После этого узел, на который указывает r можно исключить (r:=r^.left).

[ Назад | Вперед ]

Хостинг от uCoz