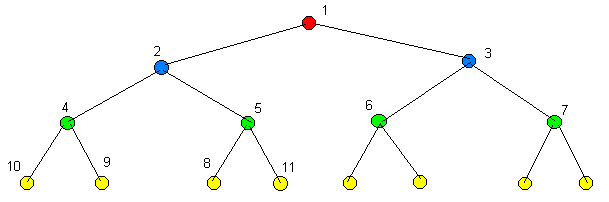
Рисунок 4.1 – Двоичная пирамида
4. Деревья
Существует несколько определений того, что такое дерево. Например, дерево – это лес, состоящий из одного связного компонента (т.е. из одного дерева) (рекурсивное определение). Или (с точки зрения теории графов), дерево – это граф без циклов. Рассмотрим деревья с точки зрения структур данных, которые должны использоваться в программах и храниться в памяти.
Деревья или, в более широком смысле, древовидные структуры данных, представляют собой динамические свЯзные структуры, отличающиеся от списков тем, что система связей не носит линейного характера, а образует ветви, подобно природному дереву (откуда и произошло название этой структуры данных).
Эти структуры данных в общем случае можно разделить на две группы, которые отличаются друг от друга способом построения и (как следствие) реализацией процедур обработки – собственно деревья и пирамиды (или "кучи"). Но у обеих этих групп сохраняется общий древовидный характер и часто их объединяют под общим коротким названием "деревья". Отличие пирамид от деревьев (и значения термина "куча") будет рассмотрено позже.
Обычно предполагается, что дерево – это неориентированная структура данных, но при реализации связей, аналогичной спискам, направление (т.е. ориентация) задаётся автоматически. Кроме того, некоторые алгоритмы обработки деревьев предполагают, что дерево является ориентированным (что не всегда удобно).
Классификация. Существует очень большое количество видов древовидных структур данных, которые можно классифицировать по нескольким различным признакам. Одно такое разделение уже было приведено – деревья и пирамиды.
Из других признаков классификации следует указать (в 1-ю очередь) число ветвей, отходящих от корня дерева. Деревья могут быть:
— двоичными (или бинарными) – имеющими не более двух ветвей (примеров таких деревьев очень много, они будут приведены позже);
– с числом ветвей больше 2 – часто такие деревья называют мультивариантными (многопутевыми) или K-деревьями (т.е. K-мерными). Примерами могут быть 2-3-деревья (и им подобные), Б-деревья (различные деревья Байера с подвариантами, например, дерево Байера-МакКрейта, Байера-Баума) и т.п. Видов K-деревьев очень много (свыше 40 различных древовидных структур для представления многомерной информации: R-Tree, R+-Tree, Hilbert R-Tree, hB-Tree, hBII-Tree, BV-Tree, BD-Tree, GBD-Tree, G-Tree, SKD-Tree, kd-Tree, kd2B-Tree, BSP-Tree, LSD-Tree, P-Tree, TR-Tree, Cell-Tree, Quadtree, Grid File, Z-Hashing, SS-Tree).
Важным признаком является состояние сбалансированности дерева и способы его достижения. Деревья могут быть:
– сбалансированными;
– идеально сбалансированными (отличие этих двух первых состояний будет рассмотрено позже);
– вырожденными;
– отличающимися более или менее сильно от сбалансированных и от вырожденных.
Автоматическая балансировка дерева выполняется, например, для АВЛ-деревьев, красно-чёрных деревьев (все эти деревья являются двоичными), Б-деревьев и некоторых других видов деревьев.
Ещё один важный признак классификации – применение деревьев (хотя не всегда из названия дерева следует, что оно применяется именно с этой целью). В качестве примера можно указать деревья поиска или сортировки, но из названия "дерево поиска" не следует, что оно применяется только для поиска.
Отдельные типы деревьев применяются для решения специальных задач, например остовные деревья на графах (каркасы графов, Spanning Tree) или PATRICIA-деревья (Practical Algorithm To Retrieve Information Coded In Alphanumeric), используемые для поиска данных на основе их поразрядного двоичного представления.
Несколько несвязанных между собой деревьев образуют структуру данных, которая называется "лес" (иногда её называют "бор").
4.1 Двоичные деревья поиска
Ещё раз дадим определение дерева как структуры данных.
Дерево — динамическая нелинейная структура данных, каждый элемент которой содержит собственно информацию (или ссылку на то место в памяти ЭВМ, где хранится информация) и ссылки на несколько (не менее двух) других таких же элементов. Для двоичного (бинарного) дерева таких ссылок две: на правый соседний и левый соседний элементы.
В общем случае данные, хранящиеся в дереве, не обязаны быть упорядочены каким-либо образом. Но часто требуется соблюдение упорядоченности по некоторому принципу. Именно по такому принципу упорядоченности и отличаются "пирамиды" и "деревья":
– пирамида ("куча") – древовидная структура данных, в которой значения всех узлов, размещённых на одном уровне, больше (или меньше) значений узлов, размещённых на выше лежащем уровне (см. рисунок);

– дерево – древовидная структура данных, в которой значения всех узлов, размещённых правее некоторого узла, больше значений узлов, размещённых левее, причём это справедливо как для всего дерева, так и для любой его части (см. рисунок). Здесь необходимо сделать одно существенное уточнение: по указанному принципу строится дерево, получившее название "двоичного дерева поиска" (Binary Search Tree, BST), т.е. дерево, в котором очень удобно искать данные, причём с высокой эффективностью этого поиска. В дальнейшем под двоичными деревьями будут подразумеваться именно двоичные деревья поиска.
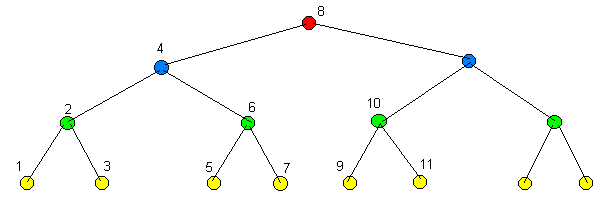
Как видно из сравнения рисунков 4.1 и 4.2, структура у пирамиды и дерева практически одинакова, отличаются они только характером размещения данных.
Также на этих рисунках видны и связи между элементами деревьев (узлами), похожие на связи между звеньями списка. Чем же отличается двоичное дерево от двусвязного списка? Иногда ничем, не только от двусвязного, но и от односвязного списка. Основное отличие - у списка соседними являются предшествующий и последующий элементы, и структура линейна; а у двоичного дерева поиска соседними являются элементы с меньшим и большим ключом, и структура, в общем случае ветвящаяся - в виде дерева, откуда она и получила свое название. Кроме того, любая часть дерева по своей структуре повторяет всё дерево в целом, т.е. дерево (любое, не только двоичное) – это рекурсивная структура данных (фактически дерево можно считать фрактальной структурой).
Нужно помнить, что дерево – это только метод логической организации информации в памяти, а память – линейна.
В случае, если информация хранится в произвольном (и неизвестном программисту) месте памяти, а ключ и информация – разные понятия (иногда они могут и совпадать), структура узла дерева может быть представлена следующим образом:

Этой структуре соответствует набор типов на языке Паскаль:
И на языках Си/Си++:
struct node
{
int key; // Ключ, по которому строится дерево
float data; // Полезные данные (могут быть любого типа)
node *left, *right; // Указатели на соседние узлы
};
Двоичное дерево, образованное такими элементами, показано ниже.
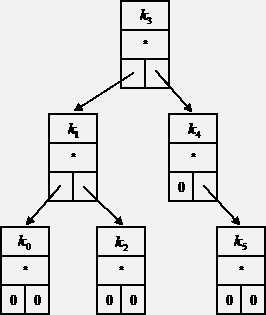
Элемент дерева получил название "узел" (node). Единственный начальный элемент (откуда дерево развивается) – корень (root). Фрагмент (часть) дерева – поддерево или ветвь. Узел, от которого не отходят ветви – конечный или терминальный узел, иногда его называют листом. Как видно на рисунках, узлы располагаются по уровням. Количество уровней – высота дерева (иногда вместо высоты используют термин "глубина"). Поскольку дерево – рекурсивная структура данных, то любой его узел может считаться корнем какой-либо ветви, в том числе пустой.
Области применения деревьев: для хранения информации, как таковой; в процедурах поиска и сортировки; для описания хранения файлов на дисковых носителях; при построении эффективных кодов для сжатия информации (коды Шеннона–Фано и Хаффмэна).
Преимущество двоичных деревьев поиска: в случае, если дерево отсортировано (а это дерево именно такое), то операция поиска выполняется быстро, с эффективностью, близкой к эффективности двоичного поиска.
4.2 Операции с деревьями
Для деревьев имеются те же основные операции, что и для списков – добавление элемента, удаление, прохождение (просмотр) и поиск элементов. Кроме них можно использовать операции принудительной балансировки, подсчёта числа узлов в дереве, измерения высоты дерева, поиска ближайшего общего корня (ближайшего общего предка – Nearest Common Ancestor (nca)) для двух элементов (в многопутевых деревьях – для более чем двух элементов). При балансировке деревьев используются операции поворотов (вращений), простых и двойных, левых и правых.
Поскольку дерево – рекурсивная структура данных, то наиболее эффективными при работе с деревьями оказываются рекурсивные процедуры. Хотя возможно применение и нерекурсивных процедур. Рассмотрим разные варианты построения этих процедур.
4.2.1 Добавление узла в дерево
Рассмотрим принцип построения дерева при занесении в него информации. Пусть последовательно вводятся записи с ключами 70, 60, 85, 87, 90, 45, 30, 88, 35, 20, 86, 82.
1. Корень – 70;
2. 60<70, следовательно новый узел будет расположен слева от 70;
3. 85>70, следовательно новый узел будет расположен справа от 70;
4. 87>70, следовательно 87 будет находиться в правой ветви; 87>85, следовательно 87 будет расположен справа от 85. И т. д.
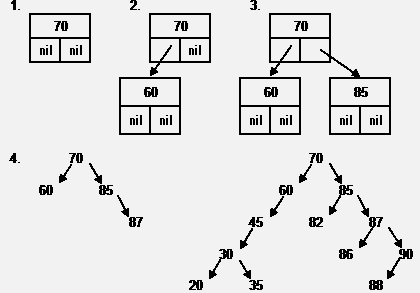
При поступлении очередной записи с ключом k, этот ключ сравнивают, начиная с корня, с ключом очередного узла. В зависимости от результата сравнения, процесс продолжают в левой или правой ветви до тех пор, пока не будет достигнут один из узлов, с которым можно связать входящую запись. В зависимости от результата сравнения входящего ключа с ключом этого узла, входящая запись будет размещена слева или справа от него и станет новым терминальным узлом.
Рекурсивная процедура добавления узла в дерево на языке "Паскаль"procedure addnode_r(r, prev: ptr; newkey: integer; newdata: info); begin
begin
r^.left := nil; r^.right := nil; r^.key := newkey; r^.data := newdata; if tree = nil then
begin
exit if newkey < r^.key then
|
Процедура добавляет информацию в двоичное дерево, отслеживая указатели на узлы и выбирая левые или правые ветви, в зависимости от ключа, пока не будет найдено соответствующее место в иерархии дерева.
Аргументы процедуры:
- указатель на корень дерева или ветви, в котором ищется место для нового узла;
- указатель на предыдущий узел;
- ключ;
- сохраняемые данные или указатель на них.
При первом вызове второй аргумент может быть равен nil.
Фактически этот процесс сортирует ключ, прежде чем добавить узел в дерево. Это вариант алгоритма сортировки методом простых вставок. При построении нового дерева или обслуживании уже упорядоченного дерева рекомендуется добавлять новые узлы именно такой процедурой.
Рассмотренная процедура использует ранее опредёленный указатель на дерево tree, которому необходимо присвоить значение nil перед первым вызовом этой процедуры (поскольку оно проверяется в строке if tree = nil ...). Приведём пример аналогичной функции на языке Си++, у которой такой же указатель является аргументом (это позволяет избежать использования глобальных структур данных):
void add_node(node*& tree, node*& r, node*& prev, node& buf)
{
if (r == NULL)
{
r = new node;
r->left = NULL;
r->right = NULL;
r->key = buf.key;
r->data = buf.data;
if (tree != r)
if (buf.key < prev->key)
prev->left = r;
else
prev->right = r;
return;
}
if (buf.key < r->key)
add_node(tree, r->left, r, buf);
else
add_node(tree, r->right, r, buf);
}
Аргументы этой функции:
tree – указатель на всё дерево;
r – указатель на некоторый текущий узел;
prev – указатель на узел, "родительский" для r;
buf – буферная структура данных типа node, содержащая вводимые данные.
Перед первым вызовом указатель tree должен быть обнулён, а сам вызов может быть следующим:
tree = NULL;
node buf;
// ...
buf.key = ... // Ввод данных в буферную область памяти
buf.data = ...
// ...
add_node(tree,tree,tree,buf);
4.2.2 Прохождение дерева
Прохождение дерева, т.е. последовательное обращение ко всем его узлам может выполняться с разными целями: просмотр (т.е. вывод на дисплей), сохранение в файл, поиск. Наиболее просто реализуется прохождение с целью просмотра.
Порядок следования узлов дерева при его прохождении зависит от того, каким образом нужно организовать доступ к узлам. Процесс получения доступа ко всем узлам - прохождение дерева.
Существует три способа прохождения дерева:
1. Последовательный – дерево проходится, начиная с левой ветви вверх к корню, затем к правой ветви;
2. Нисходящий – от корня к левой ветви, затем к правой;
3. Восходящий – проходится левая ветвь, затем правая, затем корень.
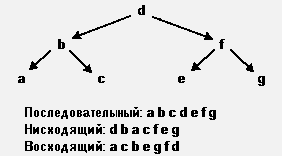
Под корнем здесь понимается как корень всего дерева, так и корень текущей ветви (поддерева).
Последовательный способ удобен для сортировки данных. Хотя двоичное дерево не обязательно должно быть отсортировано (т.е. быть двоичным деревом поиска), во многих практических случаях это требуется. Порядок сортировки дерева определяется методом, которым дерево будет проходиться. Фактически сортировка как таковая для двоичного дерева поиска не требуется, поскольку при последовательном просмотре данные ужЕ оказываются отсортированными по возрастанию.
Нисходящий способ удобен для сохранения дерева (т.е. данных, в нём хранящихся) в файл так, чтобы при последующем считывании была бы полностью восстановлена структура дерева.
Рекурсивные процедуры прохождения дерева в последовательном (inorder), нисходящем (preorder) и восходящем (postorder) порядках на языке "Паскаль"begin
inorder(r^.left); writeln( ... ); {Вывод информации} inorder(r^.right) procedure preorder(r:ptr); begin
writeln( ... ); {Вывод информации} preorder(r^.left); preorder(r^.right) procedure postorder(r:ptr); begin
postorder(r^.left); postorder(r^.right) writeln( ... ); {Вывод информации} |
Аргумент этих процедур – указатель на корень ветви, которую требуется найти. Если нужно найти все дерево, используется указатель на корень всего дерева. Выход из рекурсивной процедуры происходит, когда встречается терминальный узел.
Аналогичные процедуры на языке Си:
void inorder(node* r)
{
if (r == NULL) return;
inorder(r->left);
cout<<r->key<<" ";
inorder(r->right);
}
void preorder(node* r)
{
if (r == NULL) return;
cout<<r->key<<" ";
preorder(r->left);
preorder(r->right);
}
void postorder(node* r)
{
if (!r) return;
postorder(r->left);
postorder(r->right);
cout<<r->key<<" ";
}
Следует отметить, что дерево может быть организовано не только как динамическая связная структура данных, но и как массив. В зависимости от способа обхода дерева данные в элементах такого массива могут размещаться по-разному, например, при нисходящем обходе начальный элемент массива оказывается корнем дерева, а при последовательном обходе – самым левым узлом (см рисунок 4.7). При использовании массива для построения дерева могут использоваться совсем другие операции для доступа к узлам, а также существенно усложняется процесс добавления в дерево узлов, количество которых превышает размер массива.
Единственная возможность применения такого дерева – дерево с фиксированным или с заранее известным максимальным числом узлов, а единственное преимущество – очень быстрый доступ к любому узлу.
Строго говоря, содержимое любого массива при желании может интерпретироваться как дерево с соответствующим корнем.
4.2.3 Поиск узла в дереве
Поиск узла в дереве (в том числе в двоичном дереве поиска) может выполняться по такому же принципу, что и просмотр дерева, но в этом случае теряется эффективность этой структуры данных, а поиск фактически приобретает линейный характер. Для сохранения эффективности поиска следует или использовать рекурсивную функцию, аналогичную показанным выше inorder, preorder и т.п., преобразовав её так, чтобы её работа (и все рекурсивные вызовы) завершалась после нахождения требуемых данных:
void poisk1(node* r, int skey, node*& f)
{
if (r == NULL || f) return;
if (r->key == skey)
{ f = r; return; } // Выход, если нашли
else
if (skey < r->key)
poisk1(r->left, skey, f);
else
poisk1(r->right, skey, f);
}
Третий аргумент node*& f – одновременно узел, в котором находятся найденные данные, и признак успеха поиска. Перед вызовом этой функции соответствующий фактический аргумент должен быть равен нулю.
Рекурсивные процедуры и функции, при всех их достоинствах, обладают одним серьёзным недостатком – возможностью переполнения стека возврата из подпрограмм при большом количестве рекурсивных вызовов (а это может произойти при большом размере структуры данных), поэтому рассмотрим другой вариант реализации поиска – использование нерекурсивной процедуры:
Нерекурсивная функция поиска в двоичном дереве на языке "Паскаль"function search_tree(skey:integer; var tree,fnode:ptr):boolean; var
b: boolean;
p := tree; if tree <> nil then repeat
if p^.key = skey then
begin
search_tree := b; fnode := q; |
Аналогичная функция на языке Си++:
void poisk2(node* r, int skey, node*& f)
{
while (r != NULL && f == NULL)
{
if (r->key == skey)
{ f = r; return; } // Выход, если нашли
else
if (skey < r->key)
r = r->left;
else
r = r->right;
}
}
Эта функция практически идентична по общей структуре предыдущей рекурсивной функции. В этом примере виден и способ преобразования рекурсивных функций в нерекурсивные: рекурсивный вызов, находящийся в конце процедуры ("хвостовая" рекурсия) заменяется на цикл (в этом примере – цикл с предусловием), а рекурсивный вызов, размещённый где-либо до конца процедуры, заменяется на оператор if.
Длительность поиска зависит от структуры дерева. Для сбалансированного дерева (изображено на рисунке) поиск аналогичен двоичному – то есть нужно просмотреть не более log2(N) узлов.
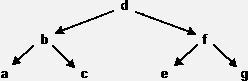
Для вырожденного дерева (изображено на рисунке) поиск аналогичен поиску в односвязном списке – в среднем нужно просмотреть половину узлов.

Используя поиск узла, можно заменить рекурсивную процедуру добавления узла на нерекурсивную:
Нерекурсивная процедура добавления нового узла в дерево на языке "Паскаль"procedure addnode2(skey:integer; var tree:ptr; newdata:^info); var
t:^info;
begin
t:=newdata; {данных} new(s); {новый} s^.key:=skey; s^.left:=nil; {узел} s^.right:=nil; s^.data:=t; if tree=nil then
|
4.2.4 Удаление узла из дерева
Удаление узла из дерева – существенно более сложный процесс, чем поиск, так как удаляемый узел может быть корневым, левым или правым. Узел может давать начало ветвям (в двоичном дереве их может быть от 0 до двух).
Наиболее простым случаем является удаление терминального узла или узла, из которого выходит только одна ветвь.
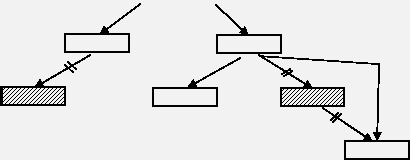
Для этого достаточно скорректировать соответствующий указатель у предшествующего узла.
Наиболее трудный случай – удаление корневого узла поддерева (или всего дерева) с двумя ветвями, поскольку приходится корректировать несколько указателей. Нужно найти подходящий узел, который можно было бы вставить на место удаляемого, причем этот подходящий узел должен просто перемещаться. Такой узел всегда существует. Это либо самый левый узел правой ветви, либо самый правый узел левой ветви.
Если это самый правый узел левой ветви, то для достижения этого узла нужно перейти в следующий от удаляемого узел по левой ветви, а затем переходить в очередные узлы только по правой ветви до тех пор, пока очередной правый указатель не будет равен nil.
Такой узел может иметь не более одной ветви.
Пример удаления из дерева узла с ключом 50.
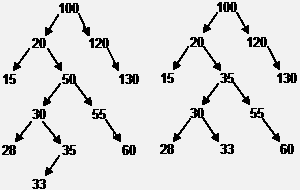
Процедура удаления узла должна различать три случая:
- узла с данным ключом в дереве нет;
- узел с заданным ключом имеет не более одной ветви;
- узел с заданным ключом имеет две ветви.
Процедура удаления узла (автор - Никлаус Вирт)
Процедура удаления узла двоичного дерева на языке "Паскаль"procedure delnode(var d: ptr; key: integer); var
procedure del1(var r:ptr); begin
begin
q^.data := r^.data; q := r; r := r^.left else
begin
else
begin
if q^.right = nil then
end |
Вспомогательная рекурсивная процедура del1 вызывается только в третьем случае. Она проходит дерево до самого правого узла левого поддерева, начиная с удаляемого узла q^, и заменяет значения полей key и data в q^ соответствующими записями полей узла r^. После этого узел, на который указывает r можно исключить (r := r^.left).
Аналогичные функции на языке Си++:
void del1(node*& r, node*& q)
{
if (r->right == NULL)
{
q->key = r->key; // Перенос данных
q->data = r->data;
q = r;
r = r->left;
}
else
del1(r->right, q);
}
void del_node(node*& d, int key)
{
node* q;
if (d == NULL)
return;
else
if (key < d->key)
del_node(d->left, key);
else
if (key > d->key)
del_node(d->right, key);
else
{
q = d;
if (q->right == NULL)
d = q->left;
else
if (q->left == NULL)
d = q->right;
else
del1(q->left, q);
delete q; // Удаление
}
}
4.2.5 Удаление всех узлов
Эта операция выполняется по тому же принципу, что и просмотр дерева:
void del_all(node*& r)
{
if (!r) return;
del_all(r->left);
del_all(r->right);
delete r;
r = NULL;
}
4.2.6 Подсчёт узлов
Это же справедливо и для подсчёта числа узлов в дереве:
void Nnodes(node* r, int& p)
{
if (r == NULL) return;
p++;
Nnodes(r->left, p);
Nnodes(r->right, p);
}
Число узлов сохраняется в аргументе p.Соответствующий ему фактический аргумент должен быть обнулён перед вызовом функции для получения правильного результата.
4.2.7 Определение высоты дерева
То же самое справедливо и при подсчёте числа уровней. После завершения работы функции высота дерева сохраняется в формальном аргументе h и в соответствующем фактическом аргументе.
void Height(node* r, int p, int& h)
{
if ( r == NULL) return;
p++;
if( r->left == NULL && r->right == NULL) // Проверка на достижение терминального узла
if (p > h)
h = p;
Height(r->left, p, h);
Height(r->right, p, h);
}
Во многих алгоритмах обработки данных, хранящихся в деревьях, предполагается, что ключи узлов должны быть уникальными, т.е. неповторяющимися. На самом деле процедуры обработки дерева допускают существование повторяющихся ключей. Следует только помнить, что в этом случае при поиске по ключу может быть найден не тот узел, который требовался, а первый встреченный узел с указанным ключом. То же самое справедливо для удаления узлов.
4.3 Сбалансированные деревья
Максимальный эффект использования двоичного дерева поиска достигается, если оно сбалансировано – когда все узлы, кроме терминальных, имеют непустые и правый и левый соседние узлы; все поддеревья, начинающиеся с одного и того же уровня, имеют одинаковую высоту.
Сбалансированное бинарное дерево – максимально широкое и низкое. Именно такими являются деревья, показанные на рисунках 4.2, 4.5, 4.7 и 4.8. Фактически все эти деревья, кроме 4.5, являются идеально сбалансированными. Менее строгое, но практически более удобное определение сбалансированности дерева – дерево является сбалансированным, если для каждого узла исходящие ветви отличаются по высоте не более, чем на одни уровень.
Обратный случай – вырожденное дерево – выродившееся в линейный односвязный список. Такое дерево получается, если заносимые в него данные упорядочены по-возрастанию (рисунок 4.9) или по-убыванию. Вырожденные деревья также получили название лево- или право-ассоциативных или "лоз", а также являются частным случаем ориентированных деревьев.
Если данные случайны, то получается дерево, в той или иной степени приближающееся к сбалансированному (рисунки 4.6, 4.11). Для двоичного идеально сбалансированного дерева с максимально возможным (для идеальной сбалансированности) числом узлов существуют простые соотношения между этим числом узлов Nузлов и высотой дерева (т.е. числом уровней) nуровней : Состояние сбалансированности (хотя бы в менее строгом смысле) часто оказывается настолько важным для тех областей, в которых деревья применяются, что для достижения этого состояния принимают специальные меры. Такими мерами являются либо та или иная операция балансировки (принудительной) дерева, в том числе включающая в себя упомянутые операции поворотов, либо использование специальных видов деревьев, обеспечивающих балансировку при каждой операции добавления или удаления узла. Основными видами таких деревьев являются АВЛ-дерево и красно-чёрное дерево.
АВЛ-дерево получило своё название по фамилиям его разработчиков – советских математиков Георгия Максимовича Адельсон-Вельского (родился 8 января 1922 г. в Самаре) и Евгения Михайловича Ландиса, которые предложили использовать такое дерево в 1962 году.
АВЛ-дерево полностью удовлетворяет менее строгому определению сбалансированности дерева. Сбалансированность достигается за счёт упомянутых выше операций поворотов (или вращений), а для сравнения высот ветвей в каждом узле двоичного дерева поиска используется дополнительное поле – признак сбалансированности ветвей (или разность их высот). Красно-чёрное дерево (RB-tree) отличается от АВЛ-дерева смыслом признака сбалансированности: вместо разности высот ветвей используется абстрактный "цвет" (красный или чёрный) и дерево строится по следующим правилам: 1. Все указатели на терминальные узлы считаются непустыми (т.е. в дереве имеются фиктивные терминальные узлы).
2. Все такие терминальные узлы считаются "чёрными". 3. Все узлы, соседние с "красными" узлами, считаются "чёрными" (т.е. запрещена ситуация с двумя "красными" узлами подряд). 4. В левой и правой ветвях дерева, ведущих от его корня к листьям, число "чёрных" узлов одинаково. Это число называется "чёрной высотой" дерева. Теоретически считается, что красно-чёрное дерево требует меньшего объёма памяти для хранения отдельного узла, чем АВЛ-дерево, т.к. для представления цвета достаточно всего одного бита. Но на практике это преимущество реализовать без потерь на дополнительные операции доступа к отдельным битам весьма сложно. Даже один из вариантов реализации красно-чёрного дерева – когда "красные" узлы обозначаются нечётными ключами, а "чёрные" узлы – чётными (или наоборот), не всегда пригоден на практике, т.к. решаемая задача может не допускать такого разделения узлов. Используемые при балансировке операции вращения фактически представляют собой переприсвоения значений указателей в узлах дерева и, как следствие, перепроведение связей между узлами, после которого высоты левой и правой ветвей оказываются одинаковыми (или отличаются не более чем на один уровень) и дерево считается сбалансированным. Суть операции вращения иллюстрируется следующим рисунком: Здесь чёрным цветом показано исходное несбалансированное дерево (ветви показаны большими треугольниками, внутри этих ветвей узлы могут быть ужЕ сбалансированы). Можно считать, что дерево "подвешено" за свой текущий корень на красный крюк. Поворот состоит в "подвеске" дерева за другой узел (который станет новым корнем) на зелёный крюк и коррекции связей: к левой ветви нового корня проводится новая связь (показана зелёным) от старого корня (эта ветка будет новой правой веткой старого корня), связь от нового корня к его старой левой ветви рвётся (зачёркнуто зелёным), и связь между старым и новым корнями меняет направление (фактически существующая связь в одном направлении уже порвана, а в обратном направлении – проводится заново). В итоге дерево "поворачивается" вокруг новой точки подвески, откуда эта операция и получила своё название. После вращения в рассматриваемом случае высоты левой и правой ветвей нового корня будут одинаковыми.
Для выполнения операции вращения может потребоваться информация о текущем узле и связанных с ним узлах (его "родителе" и его "сыне"), т.е. адреса этих узлов в памяти. Или информация о текущем узле, его "отце" и "деде", или информация о текущем узле, его "сыне" и "внуке" (в зависимости от того, рассматривается дерево как ненаправленная структура данных, или как направленная). Операция вращения может применяться не только для балансировки АВЛ- или красно-чёрных деревьев, но и обычных двоичных деревьев, не обязательно деревьев поиска. Например, один из вариантов принудительной балансировки обычного дерева заключается в преобразовании исходного дерева в лево-ассоциативное (т.е. в левую "лозу") с помощью последовательных операций вращения (см. рисунок). Затем "лоза" преобразуется в сбалансированное дерево при помощи той же операции. Б-деревья являются сбалансированными деревьями, у которых число ветвей, исходящих из узлов, может быть 2 и более. Узел, корневой для двух ветвей, содержит единственный ключ, а узел, корневой для нескольких ветвей, содержит составной ключ – несколько ключей, число которых на 1 меньше числа ветвей. Упрощенная архитектура Б-дерева показана на рисунке: В зависимости от области применения таких деревьев, полезные данные могут храниться только в их терминальных узлах (в этом случае узлы верхних уровней обеспечивают быстрый доступ по ключам к терминальным узлам), или во всех узлах, как в обычных деревьях. Существуют способы преобразования двоичного дерева в Б-дерево и наоборот. Модификацией Б-дерева является Б+ дерево – Б-дерево, у которого терминальные узлы соединены в связный список (см. рисунок): Именно по такому принципу хранятся данные в базах данных по технологии Microsoft SQL Server. Возможны и другие модификации Б-дерева, например Б++ дерево – Б+ дерево, у которого связный список формируется не только на самом нижнем уровне, но и на уровне выше. В тех случаях, когда максимальное число ветвей, исходящих из узла, ограничено, пролучаются, например, 2-3-деревья и 2-3-4-деревья. Б-деревья могут считаться частным случаем многоключевых деревьев (с переменным числом ключей). Ещё один такой частный случай – Декартово дерево. Это древовидная структура данных, в каждом узле которой содержится 2 ключа, по одному ключу она является двоичной пирамидой, а по второму ключу – двоичным деревом поиска. Более простая ситуация – двухключевое дерево, которое является двоичным деревом поиска либо только по одному из ключей, либо по сумме ключей (именно в этом случае возможно повторение сумм ключей). Такое дерево может использоваться для описания рёбер графа. При этом также возможно повторение ключей в дереве, в зависимости от структуры графа. Операции с такими двухключевыми деревьями ничем не отличаются от операций с обычными двоичными деревьями.
4.3.1 АВЛ-дерево
4.3.2 Красно-чёрное дерево
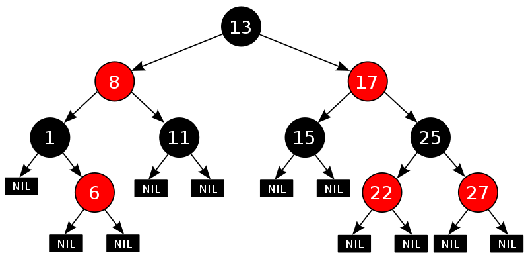
Рисунок 4.12 – Пример красно-чёрного дерева с фиктивными чёрными терминальными узлами
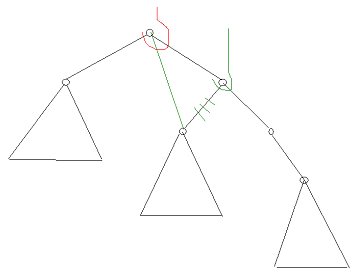
Рисунок 4.13 – Операция вращения (поворота)
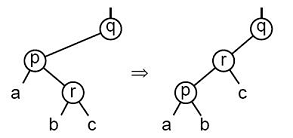
Рисунок 4.14 – Преобразование дерева в "лозу". 1-й этап
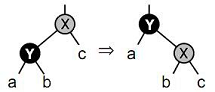
Рисунок 4.15 – Однократный правый поворот

Рисунок 4.16 – Начало преобразования "лозы" в дерево. 2-й этап
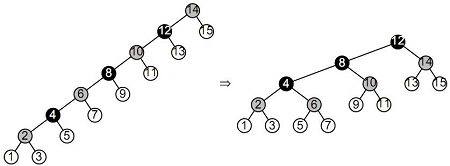
Рисунок 4.17 – Преобразование "лозы" в дерево. 3-й этап
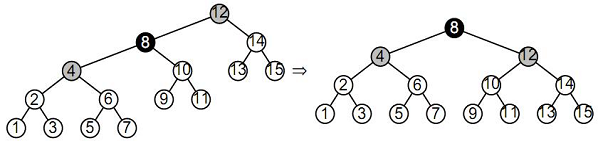
Рисунок 4.18 – Завершение преобразования "лозы" в дерево.
Рекурсивная функция построения идеально сбалансированного дерева с заданным числом узлов на языке "Паскаль"
function maketree(n_node:integer):ptr;
var
newnode: ptr;
begin
newkey, nl, nr: integer;if n_node = 0 then
end;newnode := nil
else
begin
nl := n_node div 2;
end;
nr := n_node - nl - 1; (* Ввод ключа и данных *)
read(newkey);
new(newnode);
with newnode^ do
begin
key := newkey;
end;
left := maketree(nl);
right := maketree(nr)
maketree := newnode
read(n); (* Ввод числа узлов *)
tree := maketree(n); (* Первый вызов *)
4.3.3 Б-деревья
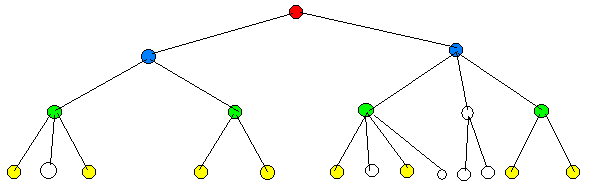
Рисунок 4.19 – Б-дерево
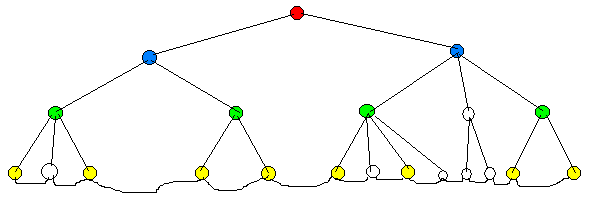
Рисунок 4.20 – Б+ дерево
4.4 Многоключевые деревья
Контрольные вопросы
1. Что представляют собой древовидные структуры данных?
2. Какие существуют виды деревьев?
3. Что представляет собой двоичное дерево?
4. В чем заключается особенность дерева как структуры данных?
5. Опишите организацию связей в дереве.
6. Перечислите основные области применения деревьев.
7. Какие операции осуществляются над деревьями?
8. В чем преимущества использования деревьев?
9. Чем отличаются двоичные деревья от списков?
10. Изобразите структуру элемента двоичного дерева.
11. Чем отличаются: сбалансированное, несбалансированное и вырожденное двоичные деревья. Проиллюстрируйте рисунками.
12. Что означают термины «сбалансированное дерево» и «идеально сбалансированное дерево»?
13. Чем вырожденное дерево отличается от односвязного списка?
14. Перечислите основные способы прохождения двоичного дерева.
15. Почему рекурсивные функции наиболее эффективны при работе с деревьями?
16. Процедуры какого характера наиболее эффективны при работе с деревьями?
17. В чем заключается вставка узла в дерево?
18. В чем заключается удаление узла из дерева?
19. Проиллюстрируйте процесс удаления узла. Как действует алгоритм в каждом из трех возможных случаев?
20. Что такое высота дерева?
21. Как сохранить сбалансированность дерева при вставке и удалении узлов?
22. Чем отличается красно-чёрное дерево от АВЛ-дерева?
23. Каковы основные особенности красно-чёрного и АВЛ-дерева?
24. На каких структурах данных могут строится деревья?